How To Use Spirograph Design Set

Mandelbrot Fractal Set up visualization in Python

Fractal:
A fractal is a curve or geometrical effigy, each office of which has the aforementioned statistical character as the whole. They are useful in modeling structures (such as snowflakes) in which similar patterns recur at progressively smaller scales, and in describing partly random or chaotic phenomena such as crystal growth and milky way germination.

In simpler words, a fractal is a never-catastrophe pattern. Fractals are infinitely complex patterns that are self-similar across unlike scales. They are created by repeating a simple process over and over in an ongoing feedback loop. Driven by recursion, fractals are images of dynamic systems – the pictures of Chaos.
Geometrically, they exist in betwixt our familiar dimensions. Fractal patterns are extremely familiar since nature is total of fractals. For instance: trees, rivers, coastlines, mountains, clouds, seashells, hurricanes, etc. Abstract fractals – such as the Mandelbrot Prepare – tin can be generated by a computer calculating a simple equation over and over.

Mandelbrot set:
The Mandelbrot fix is the set of complex numbers c for which the role does non diverge when iterated from z=0, i.due east., for which the sequence , etc., remains bounded in absolute value. In simple words, Mandelbrot set is a particular set of complex numbers which has a highly convoluted fractal boundary when plotted.

Installation of needed Python modules:

pip install pillow pip install numpy

Code #one:

from PIL import Paradigm

from numpy import complex , assortment

import colorsys

WIDTH = 1024

def rgb_conv(i):

colour = 255 * assortment(colorsys.hsv_to_rgb(i / 255.0 , ane.0 , 0.5 ))

return tuple (color.astype( int ))

def mandelbrot(ten, y):

c0 = complex (x, y)

c = 0

for i in range ( 1 , 1000 ):

if abs (c) > 2 :

render rgb_conv(i)

c = c * c + c0

render ( 0 , 0 , 0 )

img = Image.new( 'RGB' , (WIDTH, int (WIDTH / 2 )))

pixels = img.load()

for x in range (img.size[ 0 ]):

print ( "%.2f %%" % (10 / WIDTH * 100.0 ))

for y in range (img.size[ one ]):

pixels[x, y] = mandelbrot((x - ( 0.75 * WIDTH)) / (WIDTH / 4 ),

(y - (WIDTH / 4 )) / (WIDTH / 4 ))

img.show()

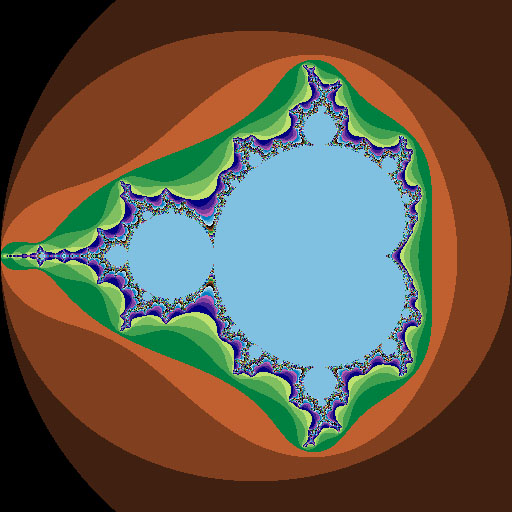
Output:

Code #ii:

from PIL import Image

xa = - 2.0

xb = 1.0

ya = - 1.5

yb = one.5

maxIt = 255

imgx = 512

imgy = 512

image = Image.new( "RGB" , (imgx, imgy))

for y in range (imgy):

zy = y * (yb - ya) / (imgy - 1 ) + ya

for x in range (imgx):

zx = 10 * (xb - xa) / (imgx - 1 ) + xa

z = zx + zy * 1j

c = z

for i in range (maxIt):

if abs (z) > 2.0 : break

z = z * z + c

image.putpixel((x, y), (i % four * 64 , i % 8 * 32 , i % sixteen * 16 ))

image.show()

Output:

How To Use Spirograph Design Set,

Source: https://www.geeksforgeeks.org/mandelbrot-fractal-set-visualization-in-python/

Posted by: garciafurk1941.blogspot.com

Share this post