How To Set The Y Intercept To Zero In Excel
This tutorial explains the syntax of the LINEST function and shows how to use it to do linear regression analysis in Excel.
Microsoft Excel is not a statistical program, however, it does have a number of statistical functions. One of such functions is LINEST, which is designed to perform linear regression analysis and render related statistics. In this tutorial for beginners, we will touch only lightly on theory and underlying calculations. Our master focus volition exist on providing you with a formula that but works and tin can be easily customized for your information.
Excel LINEST function - syntax and bones uses
The LINEST office calculates the statistics for a straight line that explains the human relationship between the independent variable and i or more dependent variables, and returns an array describing the line. The office uses the to the lowest degree squares method to find the best fit for your data. The equation for the line is as follows.
Uncomplicated linear regression equation:
y = bx + a
Multiple regression equation:
y = b1xone + b2x2 + … + bnorthxn + a
Where:
- y - the dependent variable you are trying to predict.
- x - the independent variable you are using to predict y.
- a - the intercept (indicates where the line intersects the Y axis).
- b - the slope (indicates the steepness of the regression line, i.e. the rate of alter for y equally x changes).
In its bones course, the LINEST part returns the intercept (a) and the slope (b) for the regression equation. Optionally, information technology can besides return boosted statistics for the regression analysis as shown in this example.
LINEST function syntax
The syntax of the Excel LINEST role is every bit follows:
LINEST(known_y's, [known_x's], [const], [stats])
Where:
- known_y'southward (required) is a range of the dependent y-values in the regression equation. Unremarkably, information technology is a single column or a single row.
- known_x'southward (optional) is a range of the independent x-values. If omitted, it is assumed to be the assortment {i,ii,iii,...} of the aforementioned size equally known_y's.
- const (optional) - a logical value that determines how the intercept (constant a) should be treated:
- If True or omitted, the abiding a is calculated normally.
- If FALSE, the abiding a is forced to 0 and the gradient (b coefficient) is calculated to fit y=bx.
- stats (optional) is a logical value that determines whether to output additional statistics or not:
- If TRUE, the LINEST role returns an array with additional regression statistics.
- If Imitation or omitted, LINEST only returns the intercept abiding and gradient coefficient(s).
Note. Since LINEST returns an assortment of values, it must exist entered as an array formula past pressing the Ctrl + Shift + Enter shortcut. If it is entered equally a regular formula, but the offset slope coefficient is returned.
Boosted statistics returned by LINEST
The stats statement ready to TRUE instructs the LINEST function to render the following statistics for your regression analysis:
| Statistic | Description |
| Gradient coefficient | b value in y = bx + a |
| Intercept constant | a value in y = bx + a |
| Standard fault of slope | The standard error value(s) for the b coefficient(southward). |
| Standard mistake of intercept | The standard fault value for the constant a. |
| Coefficient of determination (R2) | Indicates how well the regression equation explains the relationship among the variables. |
| Standard fault for the Y estimate | Shows the precision of the regression assay. |
| F statistic, or the F-observed value | It is used to practice the F-test for the null hypothesis to determine the overall goodness of fit of the model. |
| Degrees of freedom (df) | The number of degrees of freedom. |
| Regression sum of squares | Indicates how much of the variation in the dependent variable is explained by the model. |
| Residual sum of squares | Measures the corporeality of variance in the dependent variable that is not explained by your regression model. |
The beneath map shows the order in which LINEST returns an assortment of statistics:

In the last iii rows, the #N/A errors will appear in the tertiary and subsequent columns that are not filled with data. It is the default beliefs of the LINEST role, but if yous'd like to hibernate the error notations, wrap your LINEST formula into IFERROR every bit shown in this example.
How to utilise LINEST in Excel - formula examples
The LINEST function might exist tricky to use, especially for novices, because you should not but build a formula correctly, merely besides properly translate its output. Beneath, y'all will find a few examples of using LINEST formulas in Excel that volition hopefully help to sink the theoretical knowledge in :)
Simple linear regression: calculate gradient and intercept
To get the intercept and the slope of a regression line, you utilise the LINEST function in its simplest course: supply a range of the dependent values for the known_y's statement and a range of the contained values for the known_x's argument. The last 2 arguments tin can exist set to TRUE or omitted.
For case, with y values (sales numbers) in C2:C13 and 10 values (advertising cost) in B2:B13, our linear regression formula is as elementary as:
=LINEST(C2:C13,B2:B13)
To enter it correctly in your worksheet, select two next cells in the aforementioned row, E2:F2 in this example, type the formula, and printing Ctrl + Shift + Enter to complete it.
The formula will return the gradient coefficient in the beginning cell (E2) and the intercept constant in the second cell (F2):
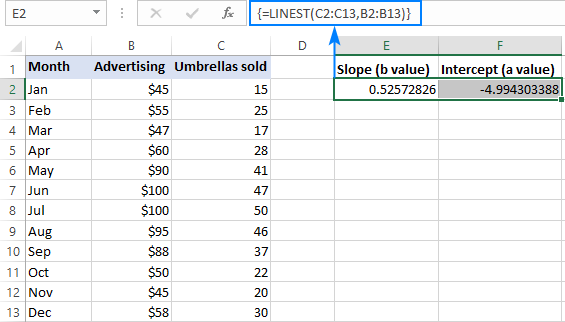
The slope is approximately 0.52 (rounded to two decimal places). It means that when ten increases by ane, y increases by 0.52.
The Y-intercept is negative -iv.99. Information technology is the expected value of y when x=0. If plotted on a graph, information technology is the value at which the regression line crosses the y-axis.
Supply the in a higher place values to a elementary linear regression equation, and yous will get the following formula to predict the sales number based on the advertising cost:
y = 0.52*x - 4.99
For instance, if you spend $50 on advertisement, you are expected to sell 21 umbrellas:
0.52*l - four.99 = 21.01
The slope and intercept values can also exist obtained separately by using the corresponding part or by nesting the LINEST formula into Index:
Slope
=Slope(C2:C13,B2:B13)
=INDEX(LINEST(C2:C13,B2:B13),1)
Intercept
=INTERCEPT(C2:C13,B2:B13)
=INDEX(LINEST(C2:C13,B2:B13),2)
As shown in the screenshot below, all three formulas yield the same results:

Multiple linear regression: slope and intercept
In case y'all have two or more independent variables, be certain to input them in next columns, and supply that whole range to the known_x's argument.
For example, with sales numbers (y values) in D2:D13, ad cost (one set of x values) in B2:B13 and average monthly rainfall (another set of x values) in C2:C13, you use this formula:
=LINEST(D2:D13,B2:C13)
Equally formula is going to return an assortment of three values (ii gradient coefficients and the intercept constant), nosotros select three face-to-face cells in the same row, enter the formula and printing the Ctrl + Shift + Enter shortcut.
Delight note that the multiple regression formula returns the slope coefficients in the opposite order of the contained variables (from right to left), that is bn, bn-1, …, b2, b1:

To predict the sales number, we supply the values returned by the LINEST formula to the multiple regression equation:
y = 0.3*xtwo + 0.19*xi- x.74
For example, with $50 spent on advertising and an average monthly rainfall of 100 mm, you lot are expected to sell approximately 23 umbrellas:
0.3*50 + 0.19*100 - 10.74 = 23.26
Simple linear regression: predict dependent variable
Autonomously from calculating the a and b values for the regression equation, the Excel LINEST function can too judge the dependent variable (y) based on the known independent variable (ten). For this, yous use LINEST in combination with the SUM or SUMPRODUCT role.
For example, hither's how you lot can summate the number of umbrella sales for the adjacent calendar month, say October, based on sales in the previous months and Oct'due south advertising budget of $fifty:
=SUM(LINEST(C2:C10, B2:B10)*{50,1})

Instead of hardcoding the ten value in the formula, you tin provide it equally a cell reference. In this example, you need to input the 1 constant in some cell too because you cannot mix references and values in an array constant.
With the ten value in E2 and the constant one in F2, either of the beneath formulas will work a treat:
Regular formula (entered by pressing Enter):
=SUMPRODUCT(LINEST(C2:C10, B2:B10)*(E2:F2))
Array formula (entered past pressing Ctrl + Shift + Enter):
=SUM(LINEST(C2:C10, B2:B10)*(E2:F2))

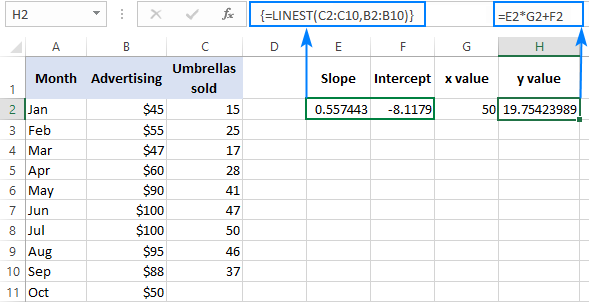
To verify the result, yous tin get the intercept and gradient for the same data, then use the linear regression formula to calculate y:
=E2*G2+F2
Where E2 is the slope, G2 is the x value, and F2 is the intercept:
Multiple regression: predict dependent variable
In case you are dealing with several predictors, i.e. a few different sets of x values, include all those predictors in the assortment constant. For example, with the advert budget of $fifty (x2) and an average monthly rainfall of 100 mm (tenone), the formula goes every bit follows:
=SUM(LINEST(D2:D10, B2:C10)*{50,100,1})
Where D2:D10 are the known y values and B2:C10 are two sets of 10 values:

Delight pay attention to the society of the x values in the assortment constant. As pointed out earlier, when the Excel LINEST part is used to do multiple regression, it returns the slope coefficients from right to left. In our case, the Advertising coefficient is returned first, and then the Rainfall coefficient. To calculate the predicted sales number correctly, you need to multiply the coefficients by the corresponding ten values, and so you put the elements of the array constant in this order: {50,100,ane}. The final element is one, because the last value returned by LINEST is the intercept that should not be changed, so yous only multiply it past 1.
Instead of using an assortment constant, you can input all the x variables in some cells, and reference those cells in your formula like we did in the previous example.
Regular formula:
=SUMPRODUCT(LINEST(D2:D10, B2:C10)*(F2:H2))
Array formula:
=SUM(LINEST(D2:D10, B2:C10)*(F2:H2))
Where F2 and G2 are the x values and H2 is ane:

LINEST formula: boosted regression statistics
As you lot may remember, to get more than statistics for your regression analysis, yous put Truthful in the terminal argument of the LINEST part. Practical to our sample data, the formula takes the following shape:
=LINEST(D2:D13, B2:C13, True, TRUE)
Every bit we have 2 independent variables in columns B and C, we select a rage consisting of 3 rows (two ten values + intercept) and 5 columns, enter the above formula, press Ctrl + Shift + Enter, and get this result:
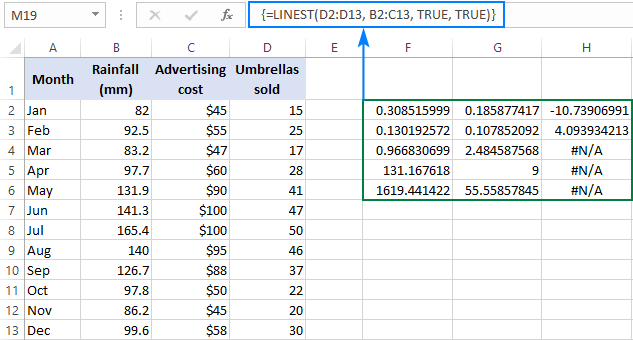
To go rid of the #N/A errors, you lot can nest LINEST into IFERROR similar this:
=IFERROR(LINEST(D2:D13, B2:C13, TRUE, TRUE), "")
The screenshot below demonstrates the result and explains what each number means:

The slope coefficients and the Y-intercept were explained in the previous examples, and so let's have a quick look at the other statistics.
Coefficient of determination (Rtwo). The value of Rtwo is the result of dividing the regression sum of squares by the total sum of squares. It tells you how many y values are explained past x variables. It can exist any number from 0 to i, that is 0% to 100%. In this example, R2 is approximately 0.97, meaning that 97% of our dependent variables (umbrella sales) are explained by the independent variables (ad + average monthly rainfall), which is an first-class fit!
Standard errors. By and large, these values show the precision of the regression analysis. The smaller the numbers, the more sure you can be about your regression model.
F statistic. You utilise the F statistic to support or reject the null hypothesis. It is recommended to use the F statistic in combination with the P value when deciding if the overall results are significant.
Degrees of freedom (df). The LINEST function in Excel returns the residual degrees of liberty, which is the total df minus the regression df. You tin can utilize the degrees of freedom to get F-disquisitional values in a statistical table, and and so compare the F-critical values to the F statistic to determine a confidence level for your model.
Regression sum of squares (aka the explained sum of squares, or model sum of squares). Information technology is the sum of the squared differences between the predicted y-values and the mean of y, calculated with this formula: =∑(ŷ - ȳ)2. Information technology indicates how much of the variation in the dependent variable your regression model explains.
Residual sum of squares. It is the sum of the squared differences betwixt the bodily y-values and the predicted y-values. Information technology indicates how much of the variation in the dependent variable your model does not explicate. The smaller the residuum sum of squares compared with the total sum of squares, the better your regression model fits your information.
5 things you lot should know about LINEST function
To efficiently utilise LINEST formulas in your worksheets, you may want to know a bit more than near the "inner mechanics" of the function:
- Known_y's and known_x's. In a simple linear regression model with only one set of x variables, known_y's and known_x's can be ranges of any shape as long as they accept the aforementioned number of rows and columns. If you practice multiple regression analysis with more than ane set up of contained 10 variables, known_y's must exist a vector, i.e. a range of one row or i cavalcade.
- Forcing the constant to zero. When the const argument is True or is omitted, the a abiding (intercept) is calculated and included in the equation: y=bx + a. If const is ready to FALSE, the intercept is considered to exist equal 0 and omitted from the regression equation: y=bx.
In statistics, it has been debated for decades whether it makes sense to forcefulness the intercept abiding to 0 or not. Many credible regression assay practitioners believe that if setting the intercept to zilch (const=Imitation) appears to be useful, so linear regression itself is a wrong model for the data set. Others suppose that the constant tin can exist forced to zippo in certain situations, for instance, in the context of regression discontinuity designs. In full general, it is recommended to become with the default const=TRUE or omitted in most cases.
- Accuracy. The accuracy of the regression equation calculated by the LINEST role depends on the dispersion of your data points. The more linear the data, the more accurate the results of the LINEST formula.
- Redundant 10 values. In some situations, one or more independent x variables might take no additional predictive value, and removing such variables from the regression model does not affect the accuracy of the predicted y values. This miracle is known equally "collinearity". The Excel LINEST function checks for collinearity and omits any redundant x variables that information technology identifies from the model. The omitted ten variables tin be recognized by 0 coefficients and 0 standard error values.
- LINEST vs. Slope and INTERCEPT. The underlying algorithmic of the LINEST function differs from the algorithm used in the SLOPE and INTERCEPT functions. Therefore, when the source data is undetermined or collinear, these functions may return different results.
Excel LINEST role not working
If your LINEST formula throws an fault or produces a wrong output, chances are it'due south because of one of the following reasons:
- If the LINEST office returns just one number (gradient coefficient), almost likely y'all accept entered it as a regular formula, not an array formula. Be sure to press Ctrl + Shift + Enter to consummate the formula correctly. When you do this, the formula gets enclosed in the {curly brackets} that are visible in the formula bar.
- #REF! error. Occurs if the known_x's and known_y's ranges have different dimensions.
- #VALUE! error. Occurs if known_x'due south or known_y's contains at to the lowest degree one blank cell, text value or text representation of a number that Excel does not recognize as a numeric value. Also, the #VALUE mistake occurs if the const or stats argument cannot be evaluated to Truthful or Faux.
That's how you use LINEST in Excel for a uncomplicated and multiple linear regression analysis. To have a closer look the formulas discussed in this tutorial, you are welcome to download our sample workbook beneath. I give thanks you for reading and hope to run across y'all on our blog next week!
Practice workbook for download
Excel LINEST part examples (.xlsx file)
Yous may likewise be interested in
Source: https://www.ablebits.com/office-addins-blog/2018/07/25/excel-linest-function-formula-examples/

0 Response to "How To Set The Y Intercept To Zero In Excel"
Post a Comment